Python Programming

Fibonacci Series in Python

Introduction

The Fibonacci sequence is a well-known integer number series. The sequence appears in many problems naturally and has a great recursive definition. Learning how to produce it is an important step toward grasping recursion for the pragmatic programmer.

Examining the Recursion Behind the Fibonacci Sequence

The Fibonacci sequence generation is a classic recursive problem. Recursion occurs when a function refers to itself in order to deconstruct the problem it is attempting to solve. Each function call reduces the problem until it reaches a base case, at which point it returns the result to each intermediate caller until it provides the result to the original caller.

Generating the Fibonacci Sequence Recursively in Python

To generate the Fibonacci sequence, the most common and simplest algorithm requires you to write a recursive function that calls itself as many times as necessary until it computes the desired Fibonacci number.

def fibonacci_of(n):
if n in {0, 1}: # Base case
return n
return fibonacci_of(n - 1) + fibonacci_of(n - 2) # Recursive case

[fibonacci_of(n) for n in range(15)]

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377]

The base case is checked first within Fibonacci of(). Then you return the sum of the values obtained by executing the function with the two preceding n values. At the end of the example, the list comprehension generates a Fibonacci sequence using the first fifteen numbers.

Optimizing the Recursive Algorithm for the Fibonacci Sequence

There are at least two ways you may employ to improve the efficiency of the algorithm used to construct the Fibonacci sequence—that is, to make it take less time to compute. These strategies ensure that you do not repeatedly compute the same numbers, which is what made the previous algorithm wasteful. They are known as memoization and iteration.

Memoization

By storing previously calculated results in a cache, memoization speeds up the execution of expensive recursive procedures. When the same input is given again, the function only needs to seek up the appropriate result and return it, rather than running the computation twice. These outcomes can be referred to as cached or memoized:

This optimization could be translated into Python code as follows:

cache = {0: 0, 1: 1}

def fibonacci_of(n):
if n in cache: # Base case
return cache[n]
# Compute and cache the Fibonacci number
cache[n] = fibonacci_of(n - 1) + fibonacci_of(n - 2) # Recursive case
return cache[n]

[fibonacci_of(n) for n in range(15)]

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377]

Exploring an Iterative Algorithm

An iterative algorithm can be used to compute the number at position n in the Fibonacci sequence.

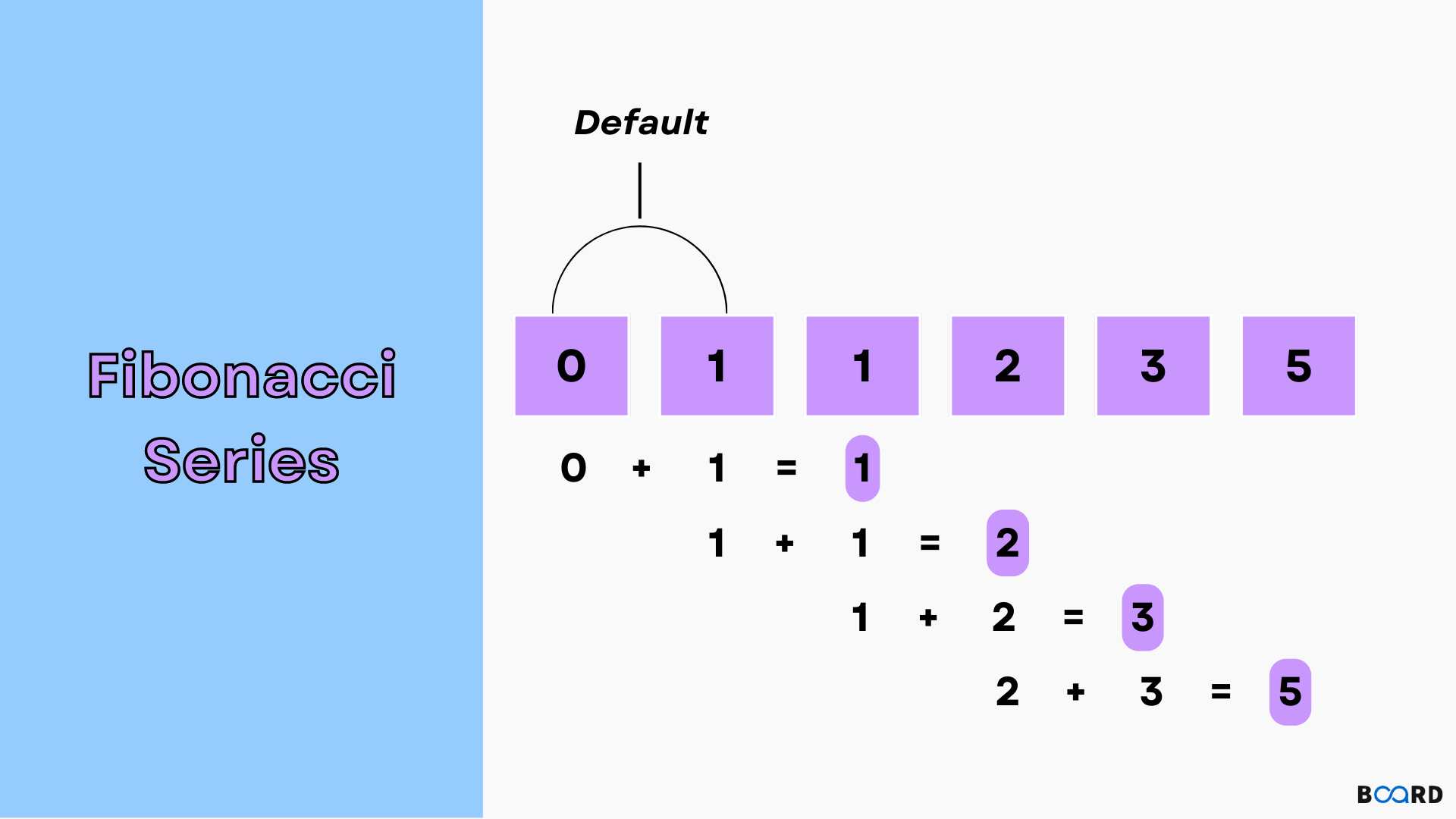
In the diagram below, the bolded purple numbers represent the new numbers that must be calculated and added to cache in each iterative step:

To find the Fibonacci number at location n, save the first two integers in the series, 0 and 1, in cache. Then, calculate the following integers sequentially until you can return cache[n].

Generating the Fibonacci Sequence in Python

Using Recursion and a Python Class

Your first method for producing the Fibonacci sequence will involve the usage of a Python class and recursion. The class has an advantage over the previously seen memoized recursive function in that it retains state and behavior (encapsulation) together within the same object.

# fibonacci_class.py

class Fibonacci:
def __init__(self):
self.cache = [0, 1]

def __call__(self, n):
# Validate the value of n
if not (isinstance(n, int) and n >= 0):
raise ValueError(f'Positive integer number expected, got "{n}"')
# Check for computed Fibonacci numbers
if n < len(self.cache):
return self.cache[n]
else:
# Compute and cache the requested Fibonacci number
fib_number = self(n - 1) + self(n - 2)
self.cache.append(fib_number)

return self.cache[n]

Using Iteration and a Python Function

The previous sections' examples implement a recursive solution that employs memoization as an optimization strategy. In this section, you will write an iterative function. The following code runs an iterative version of your Fibonacci sequence algorithm:

fibonacci_func.py

def fibonacci_of(n):
# Validate the value of n
if not (isinstance(n, int) and n >= 0):
raise ValueError(f'Positive integer number expected, got "{n}"')

# Handle the base cases
if n in {0, 1}:
return n
previous, fib_number = 0, 1
for _ in range(2, n + 1):
# Compute the next Fibonacci number, remember the previous one
previous, fib_number = fib_number, previous + fib_number

return fib_number

Conclusion

The Fibonacci sequence can help you better comprehend recursion. You have learned about the Fibonacci sequence in this course. You have also learned about some standard sequence generation techniques and how to transfer them into Python code.

The Fibonacci sequence can be a good springboard and entry point into the domain of recursion, which is a fundamental programming ability.