Sets in Python
Introduction
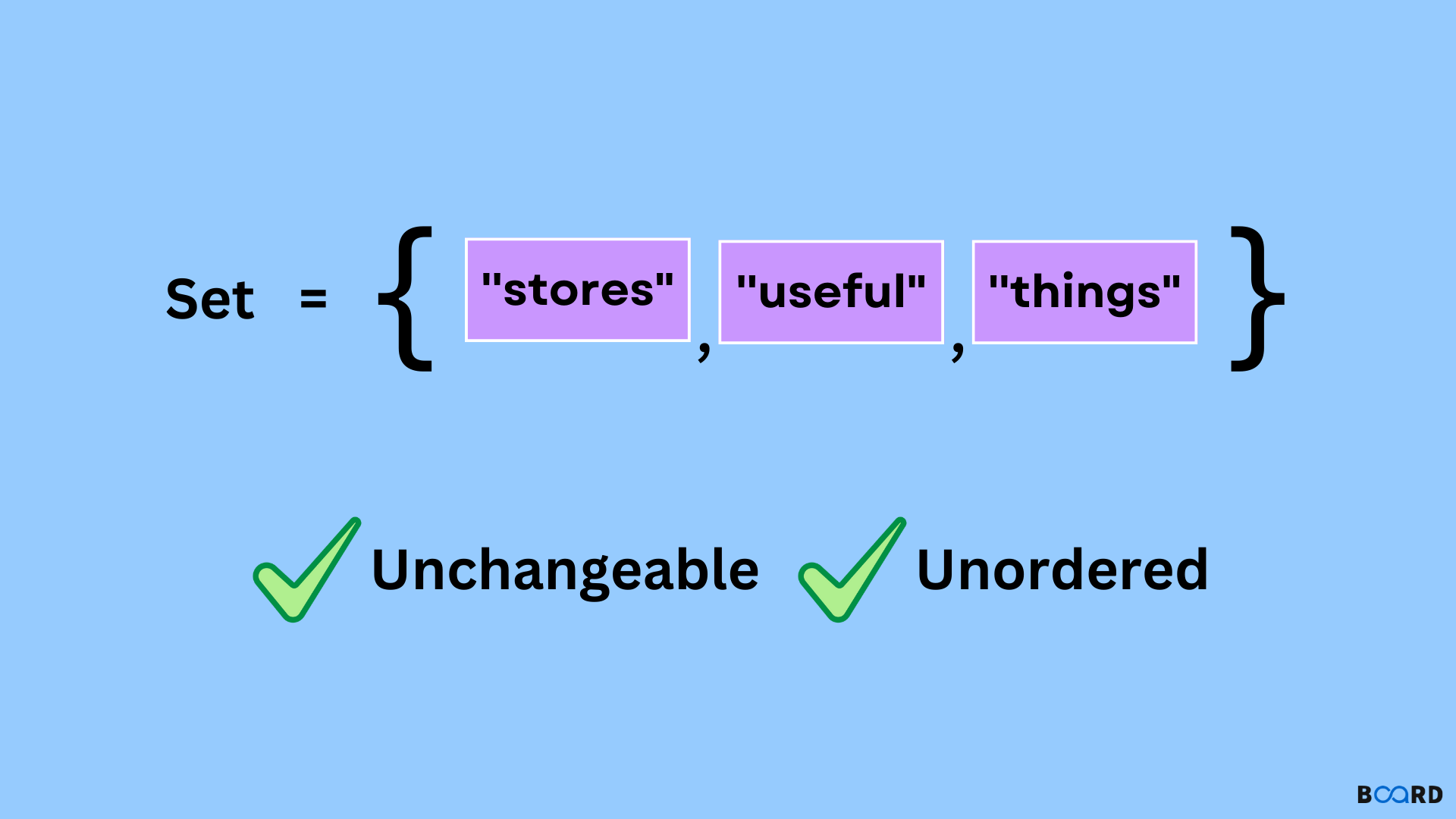
In math, a set is a group of things that are not necessarily in any specific order. With the additional constraints listed below, a Python set is identical to this mathematical definition.
A set's characteristics:
The built-in data structure in Python, known as a set, has the following three features.
1) Unordered: Unlike lists, the items in a set are not maintained in the order in which they are inserted. The items will be in a different sequence every time we access the Set object. Each item in the Set won't have an index value assigned to it.
2) Immutable: Set objects must be unchangeable. The set items cannot be altered, i.e., their values cannot be changed. But we have the option to change the Set's contents. Although the elements that make up a set may be changed, the Set itself must be immutable.
3) Unique: No two elements in the set can have the same value.
Set operations
Union, intersection, difference, complement, and other mathematical operations are frequently performed in Python using sets. As seen below, we can establish a set, get at its components, and do certain mathematical operations.
Assembling a group
Using the set() function or grouping all the components inside a pair of curly braces creates a set.
Output:
When the code listed above is run, the outcome is as follows. Please take note of how the elements' relative order has altered.
Using a Set to Access Values
We are unable to access certain values within a set. All the components must be accessed at once as demonstrated above. But by iterating through the set in a loop, we can also obtain a list of distinct elements.
Output:
When the aforementioned code is run, the outcome is as follows:
Adding Items to a Set
The add() method can be used to add elements to a set. As was previously said, the newly inserted element is not associated with any particular index.
Output :
The outcome of running the aforementioned code is as follows:
Removing Item from a Set
By utilizing the discard() method, we can eliminate elements from a set. As was previously said, the newly inserted element is not associated with any particular index.
Output:
The following outcome is produced when the aforementioned code is run.
Union of Sets
A new set comprising all the unique elements from both sets is created by performing a union operation on two sets. The element "Wed" in the example below is present in both sets.
Output
The following outcome is produced when the aforementioned code is run. Note that there is only one "wed" in the outcome.
Set intersection
When two sets are intersected, a new set is created that only contains the shared elements of the two sets. The element "Wed" in the example below is present in both sets.
Output
The following outcome is produced when the aforementioned code is run. Note that there is only one "wed" in the outcome.
Set Difference
When two sets are compared, the difference operation creates a new set that only contains elements from the first set and none from the second. The element "Wed" in the example below is present in both sets, hence the result set will not contain it.
Output
The following outcome is produced when the aforementioned code is run. Note that there is only one "wed" in the outcome.
Compare Sets
It is possible to determine whether a set is a subset or superset of another set. Depending on the elements in the sets, the outcome is either True or False.
Output
The outcome of running the aforementioned code is the following:
