A quick guide to Asymptotic Analysis

Introduction

Asymptotic Analysis for computer programs generally describes their efficiency of them with machine-independent variables, These are mathematical tools used for analyzing the time complexity of the programs. Asymptotic notations are of three types. They are mentioned below:

1. Big O notation (Worst Case)
2. Theta notation (Average Case)
3. Omega notation (Best Case)

The below article clearly explains each notation in detail.

1. Big O Notation

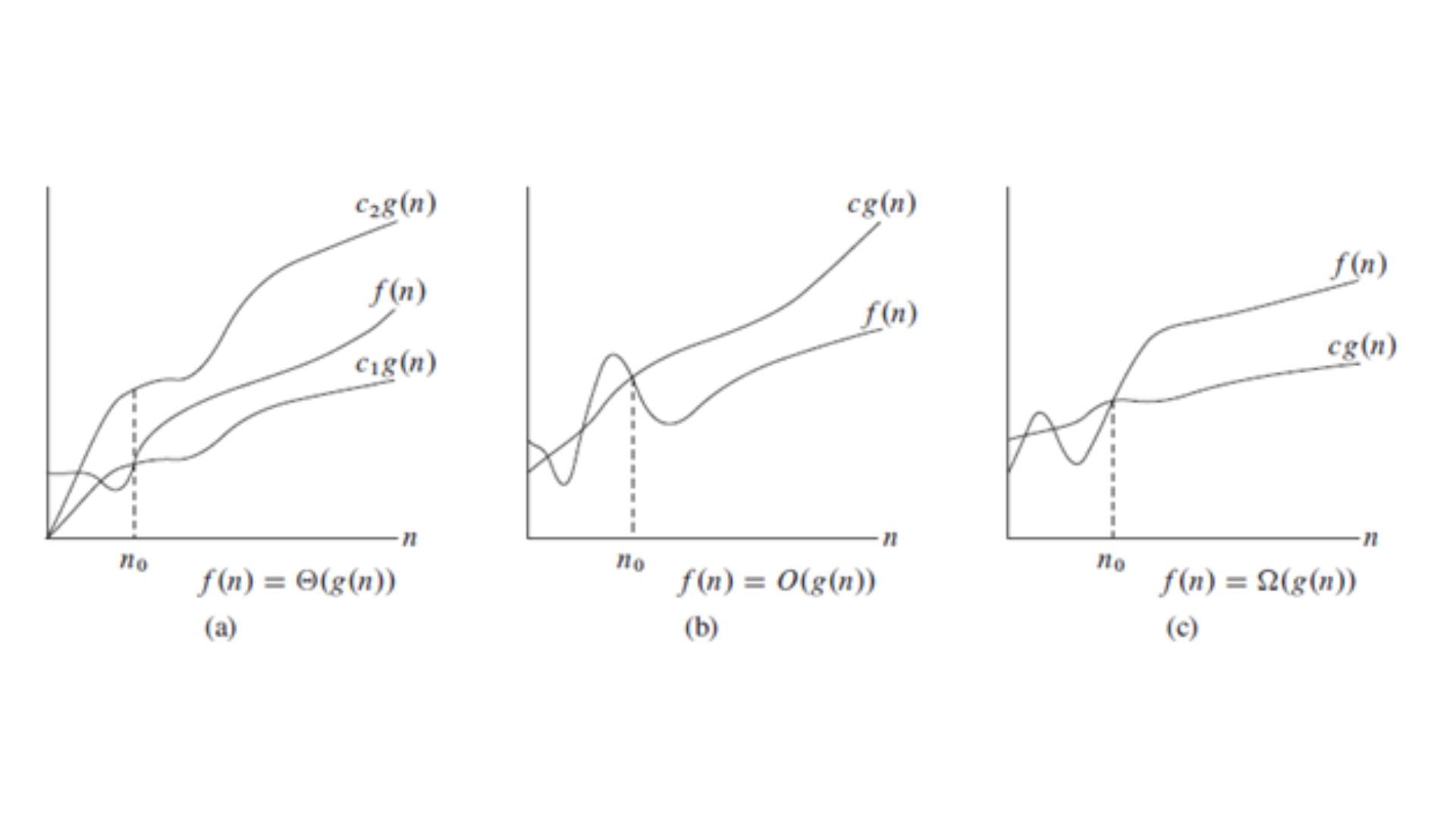
Big O notation basically represents the upper bound of the running time of an algorithm. It basically measures the time taken by the program to return the output once the input increases. Therefore it gives the worst time complexity of the program. It is generally represented as O(N), where N represents the input for the program. Mathematically,  

O(g(n)) = { f(n)}  then there exist positive constants like C and n0 such that 0 ≤ f(n) ≤ Cg(n) :  n ≥ n0 }.

Let g, f be the set of natural numbers with itself.

Big O notation is helpful in finding the worst-case time complexity of a particular program with the help of huge input.

Examples of Big O time complexity:

• Linear search: O(N), where N is the number of elements in the given array
• Binary search: O(Log N),  where N is the number of elements in the given array
• Bubble sort: O(N2),  where N is the number of elements in the given array
• O(N2)+O(N3)+O(NlogN)= O(N3),  where N is the number of elements in the given array.

2. Theta Notation

The theta notation in the asymptotic notation type describes the average case time complexity of a computer program. It is represented as Θ-Notation. It represents the both upper bound and lower bound of a running time algorithm. Mathematically, it means

Θ (g(n)) = {f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1 * g(n) ≤ f(n) ≤ c2 * g(n) for all n ≥ n0}

Examples of Theta notation in asymptotic notations:

• (N2), (N log N), (3*N2) gives average time complexity as Θ(N2)
• (N), (log N), (5*N) gives average time complexity as  Θ(N)

3. Omega Notation

Omega notation in asymptotic analysis gives the best-case time complexity of the given runtime algorithm. It gives a measure of the lower boundary of the runtime algorithm. It is generally represented as Ω-Notation. Mathematically,

Ω(g(n)) = { f(n)} then  there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }

Examples of Omega notation in asymptotic notations are:

• {(N2+N), (4*N), (N2+LogN)} gives the best time complexity as Ω(N2)

Conclusion

This article mainly explained the asymptotic notations present in finding out the efficiency of the given algorithm. There about three types of asymptotic notations Big O notation, Theta notation, and Omega notation which are worst case, the average case, and best case time complexity of the given runtime algorithm.