Understanding Algorithm: Complexity and Performance

Binary Search Tree: Explanation

Board Infinity
Board Infinity
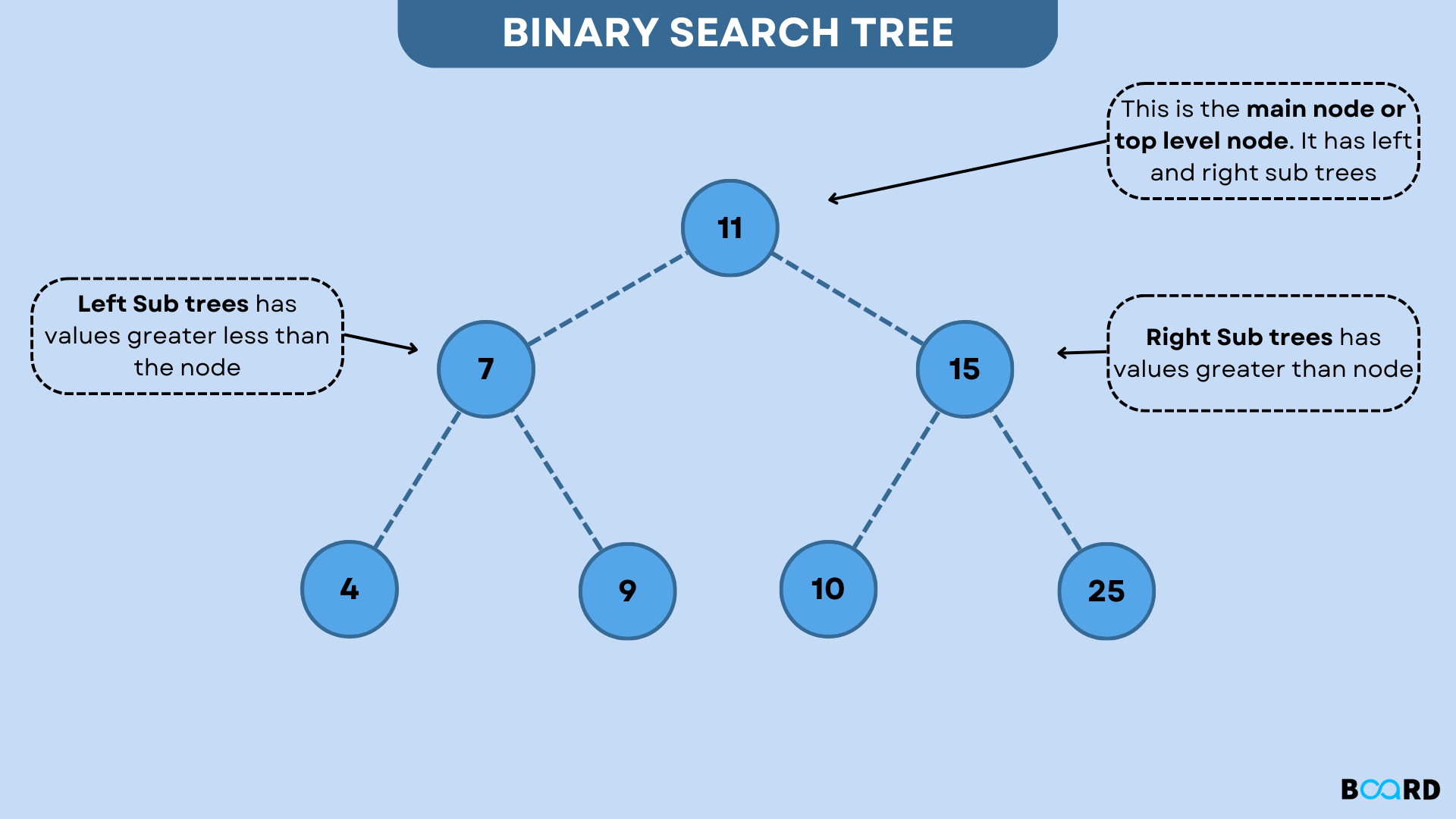
Binary Search Tree: Explanation

    A quick guide to Asymptotic Analysis

    Searching Algorithm and its Types

    What is Hashing in Data Structure?

    How to Build a TreeMap?

    Difference between Hashmap and HashTable

    A Quick Guide to Bubble Sort Algorithm

    How to find the kth smallest/largest element in an array?

    How to use Merge Sort with Linked Lists

    Finding Array Triplets with Given Sum

    What Is An Algorithm (Understanding The Ingredients)

    Tail Recursion Problem

    Stack vs Heap Memory: Key Differences

    Algorithm and Flowchart: Differences Explained

    Big O Notation: Space and Time Complexity

    Graphs in Data Structure and Algorithm

    Time Complexity: Explanation

    Binary Search Tree: Explanation

    Heap Sort Algorithm

    Time Complexity of Sorting Algorithms

    Load Factor and Rehashing

What is Binary Tree Data Structure?

A Binary Tree is a Tree data structure with no more than two children. Because each element in a binary tree can only have two children, they are commonly referred to as the left and right child.

Binary Tree Representation

A pointer to the tree's topmost node represents a Binary tree. If the tree is empty, then the root value is NULL.

A Binary Tree node is made up of the following components:

  1. Data
  2. Pointer to the left child
  3. Pointer to the right child

Basic Binary Tree Operation

  • Adding a new element.
  • Deleting an element.
  • Searching for an element.
  • Traversing an element.

Auxiliary Binary Tree Operation

  • Determining the tree's height
  • Determine the tree's level.
  • Determining the overall size of the tree.

Applications of Binary Search Tree (BST):

Because BSTs are organized, they can be used for many different things.

  • BSTs are utilized in indexing as well as multi-level indexing.
  • They are also useful in the implementation of various search algorithms.
  • It is helpful for maintaining a stream of sorted data.
  • Self-balancing BSTs are used internally to implement the TreeMap and TreeSet data structures.

Binary Search Tree: Transversal

Three different types of traversals can be made over a binary search tree. All of these traversals follow a largely similar path through the tree's nodes.

In-order

The root node's left subtree is traversed first, then the current node, and finally the right subtree of the current node. The base case, which states that an empty tree is also a binary search tree, is also represented by the code.

Syntax:

void inOrder(struct node* root) {
        // Base case
        if (root == null) {
                return;
        }
        // Travel the left sub-tree first.
        inOrder(root.left);
        // Print the current node value
        printf("%d ", root.data);
        // Travel the right sub-tree next.
        inOrder(root.right);
}

Pre-order

This traversal initially reads the current node value before traversing the left and right sub-trees.

Syntax:

void preOrder(struct node* root) {
        if (root == null) {
                return;
        }
        // Print the current node value
        printf("%d ", root.data);
        // Travel the left sub-tree first.
        preOrder(root.left);
        // Travel the right sub-tree next.
        preOrder(root.right);
}

Post-order

This traversal runs over the left and right subtrees first, then the root value. The order of the left and right subtrees remains unchanged. In all of the preceding traversals, just the position of the root changes.

Syntax:

void postOrder(struct node* root) {
        if (root == null) {
                return;
        }
        // Travel the left sub-tree first.
        postOrder(root.left);
        // Travel the right sub-tree next.
        postOrder(root.right);
        // Print the current node value
        printf("%d ", root.data);
}

write your code here: Coding Playground