Counting Sort Algorithm: Using C++

Board Infinity

Introduction

In this article we will be discussing the counting sort. Counting sort is a sorting algorithm. In technical interviews, sorting algorithms are generally asked so this article is extremely important. So, let’s begin decoding counting sort with full focus on!!

Counting sort does not sort by comparing elements. Counting sort sorts elements by storing the count of unique elements. The count is stored in an auxiliary array and the sorting is done by mapping the count as an index of the auxiliary array.

Why Counting Sort?

Yes , that’s a good question. Let’s see some characteristics of counting sort that will answer this question of yours.

Counting sort works by making the assumption about the data like it will make an assumption that data is going to be in the range of 0- 10 or 10-99 etc.
Sorting algorithm does not work by making comparisons, instead it works by hashing the values in an auxiliary array and then uses it for sorting.
Since it uses an auxiliary array.Itis a non-in place algorithm.

Don’t worry you will get it clearly with the below example:

Suppose we are give a array containing elements between 0 to 9 like:

Input = [1, 4, 1, 2, 7, 2].

Now we will make an auxiliary array to store the count of each unique element.

Now traverse this array and store the count of each element.

Input array:

Now the auxiliary array that will be storing the count of each unique element will be:

Since we have assumed that elements will be from 0 to 9 so the size of the auxiliary array will be 10.

0 1 2 3 4 5 6 7 8 9

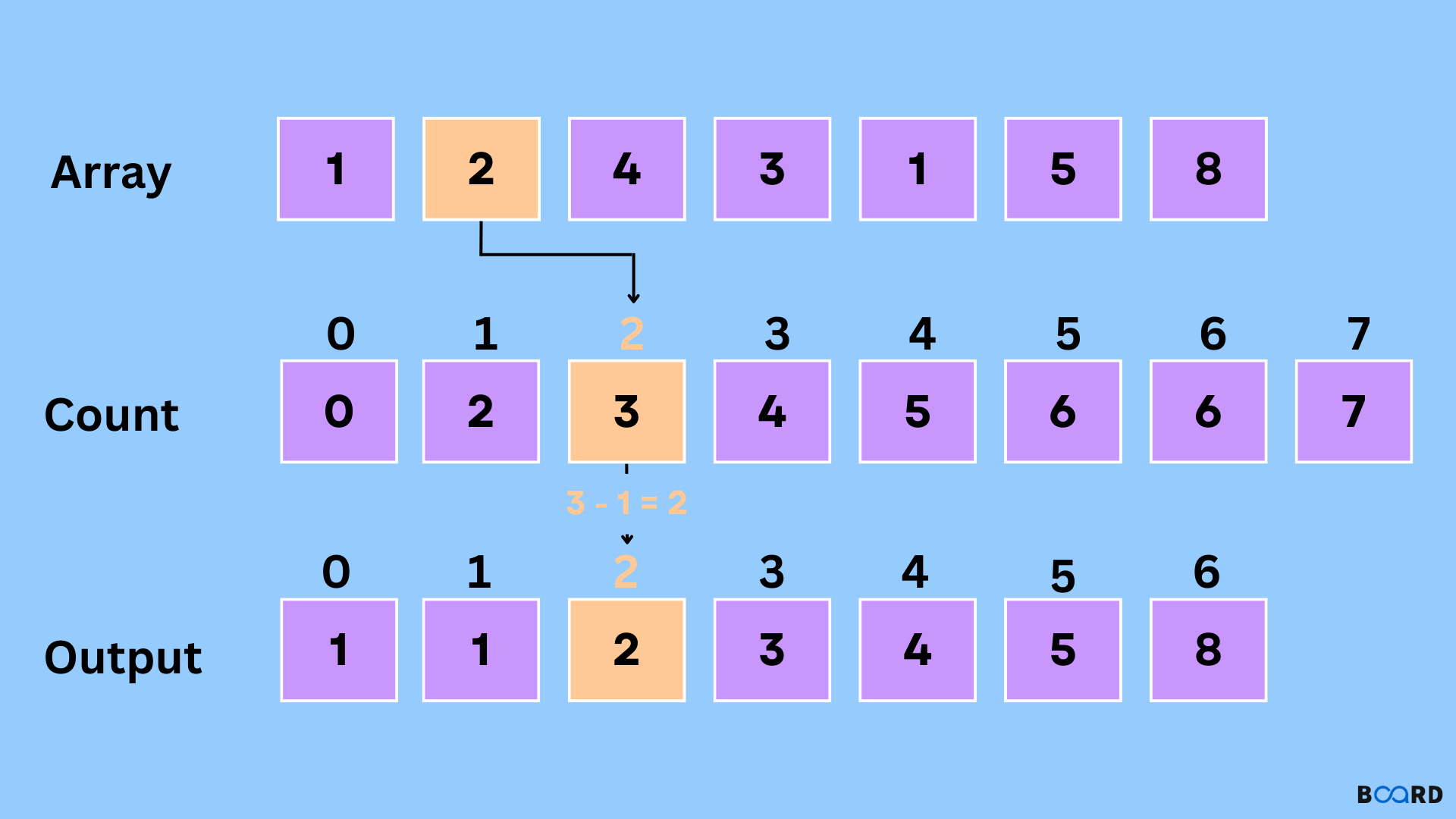
Now, Modify the count array such that each element at each index stores the sum of previous counts.

So the auxiliary array will become:

0 1 2 3 4 5 6 7 8 9

Now rotate the array clockwise for one time.Then output each element from the input sequence followed by increasing its count by 1.Process the input data: 1, 4, 1, 2, 7, 5, 2.Like the Position of 1 is 0.So, Put data 1 at index 0 in output. Increase count by 1 to place next data 1 at an index 1 greater than this index.

After placing each element at its correct position, decrease the count of that element by one.

Since I have discussed the approach now, try writing code for it on your own.I am waiting write fast!!

You tried Good! Let’s check your solution with mine below:

#include <bits/stdc++.h>
#include <string.h>
using namespace std;
#define RANGE 255

// The main function that sort
// the given string arr[] in
// alphabetical order
void countSort(char arr[])
{
// The output character array
// that will have sorted arr
char output[strlen(arr)];

// Create a count array to store count of individual
// characters and initialize count array as 0
int count[RANGE + 1], i;
memset(count, 0, sizeof(count));

// Store count of each character
for (i = 0; arr[i]; ++i)
++count[arr[i]];

// Change count[i] so that count[i] now contains actual
// position of this character in output array
for (i = 1; i <= RANGE; ++i)
count[i] += count[i - 1];

// Build the output character array
for (i = 0; arr[i]; ++i) {
output[count[arr[i]] - 1] = arr[i];
--count[arr[i]];
}

/*
For Stable algorithm
for (i = sizeof(arr)-1; i>=0; --i)
{
output[count[arr[i]]-1] = arr[i];
--count[arr[i]];
}

For Logic : See implementation
*/

// Copy the output array to arr, so that arr now
// contains sorted characters
for (i = 0; arr[i]; ++i)
arr[i] = output[i];
}

// Driver code
int main()
{
char arr[] = "boardinfinity";

countSort(arr);

cout << "Sorted character array is " << arr;
return 0;
}

Output:

Sorted character array is abdfiiinnorty

Time Complexity: O(n+k) where n is the number of elements in the input array and k is the range of input.

Auxiliary Space: O(n+k)

I hope now you must be clear with counting sort.If still feel any confusion then go through this article once more.I agree counting sort is a little bit more complex than other sorting algorithms. But after solving 2-3 problems over it you will surely master it.Happy Coding!!

Counting Sort Algorithm: Using C++

Board Infinity

OOPs (Object Oriented Programming) in C++

A Quick Guide to Encapsulation in C++

OOPs Abstraction in C++

OOPS Polymorphism with C++

Multiple Inheritance in C++

Virtual Base Class in C++

How to Perform Insertion Sort in C++?

Counting Sort Algorithm: Using C++

Bucket Sort Algorithm with C++

Implementing Binary Search in C++

Print all Permutations of given String: using C++

Sliding Window Problem – C++ Implementation

Implement Tower of Hanoi using C++

Rabin Karp Algorithm: C++ Implementation

Job Sequencing Problem with C++

Biconnected Graph Algorithm with C++

Hamiltonian Path Algorithm with C++

Introduction

Why Counting Sort?