Trie Data Structure: Explanation and Examples
What is Trie?
Trie is a sort of k-ary search tree that is used to store and search for a certain key in a set. Search complexity can be reduced to an ideal level using Trie (key length).
A well-balanced BST will require time proportional to M * log N if we store keys in a binary search tree, where N is the number of keys and M is the max. string length in the tree. The key can be searched in O(M) time using Trie. However, Trie storage requirements are penalized.
Trie is often referred to as a prefix tree or a digital tree.
Structure of Trie node
Trie has several branches at each node. Each branch stands for a potential key character. Note that the word node ends at the last node of each key. It is possible to identify a node as the end of a word using the Trie node field isEndOfWord.
The following is an easy structure that can be used to represent the English alphabet's nodes:
Insert Operation in Trie
Adding a key to Trie is an easy process.
- Each character of the input key is entered as a separate Trie node. Keep in mind that the school is an array of pointers to trie nodes on the next level.
- In array school, the key character acts as an index.
- Create a new node for the key and indicate the word's end for the last node if the input key is new or an extension of an existing key.
- Simply indicate the last node of the input key as the end of the word if it is a prefix of an already existing key in Trie.
Trie depth is determined by the key length.
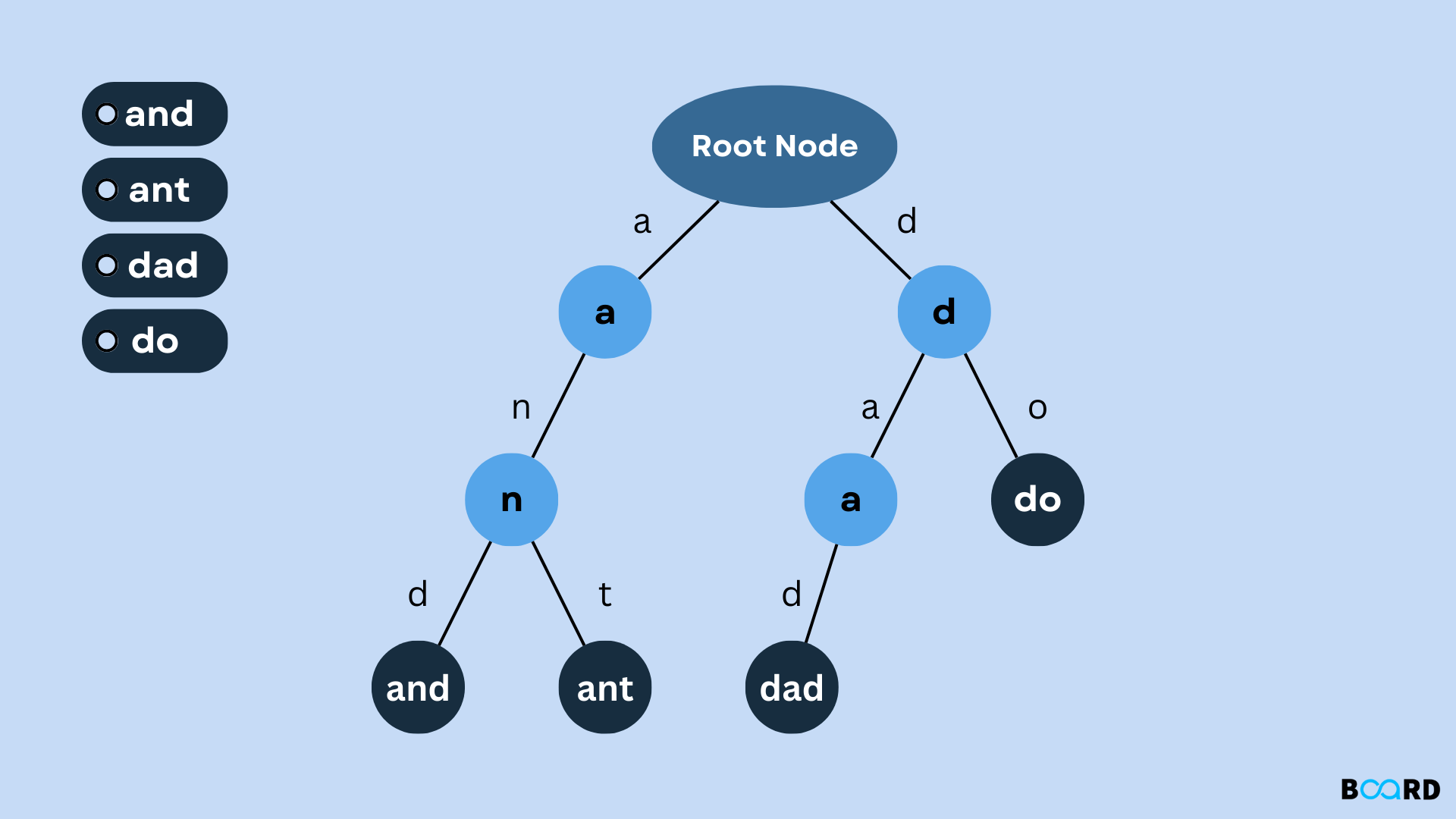
The construction of a trie using the keys shown in the example below is illustrated in the following image.
Search Operation in Trie
Key searching is similar to insert operation. However, it moves down after comparing only the characters. The lack of a key in the trie or the end of a string can cause the search to end.
- If the last node's isEndofWord field is true in the first scenario, the key is present in the trie.
- In the second example, because the key is missing from the trie, the search is over before all of the key's characters have been examined.
Note: While Trie's memory needs are O(ALPHABET SIZE * key length * N), where N is the number of keys in Trie, insert and search costs are O(key length).To reduce the trie's memory requirements, there exist effective representations of trie nodes (such as compressed trie, ternary search tree, etc.).
How is a tree data structure implemented?
- Use the TrieNode() constructor to create a root node.
- Keep a group of strings that need to be inserted into the trie in a vector of strings called arr, for example.
- Using the insert() function to insert all strings into Trie.
- Using the search() method to search strings.
Trie implementation of above approach
Output
