Java Advanced Topics and Techniques

Kadane's Algorithm with Java

Board Infinity
Board Infinity
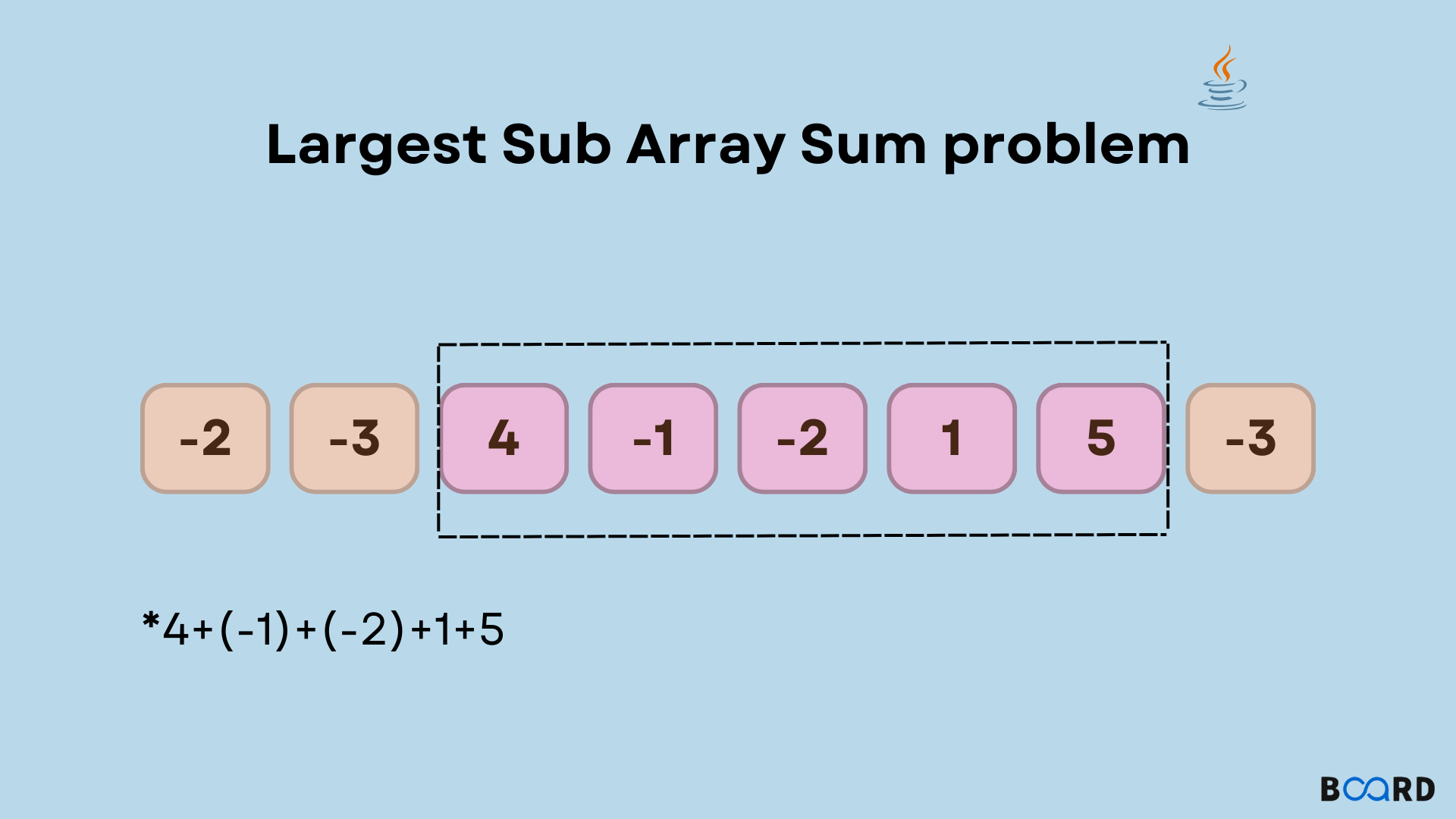
Kadane's Algorithm with Java

    Encapsulation in Java: A Comprehensive Tutorial

    String Array in Java

    Reverse an Array in Java

    Converting Character Array to String in Java

    Pojo Class in Java: How to Create?

    ListSize() in Java

    Try, Catch and Finally in Java

    Constructor Chaining in Java

    Equals and == in Java: Differences

    Abstract Class in Java

    Runnable Interface in Java

    Java Custom Exception

    Hashcode() in Java

    Understanding the difference between JDK, JRE, and JVM

    AWT and SWING in Java

    Difference between JSP and Servlet

    Servlet Life Cycle

    Java Design Pattern: Factory Method

    Collectors toMap() in Java

    Socket Programming in Java: Comprehensive Guide

    Kadane's Algorithm with Java

Introduction

Kadane’s Algorithm is used to find the subarray with the largest sum in the given array. The intuition behind this algorithm is to declare a variable ‘sum’ and keep adding the elements in the sum. And, each time you add an element to the sum, update it using the ‘max’ function.

It means that each time, the current sum and previous sum are compared. The sum is assigned the maximum value out of the previous sum and the current sum. Also, if the array contains negative elements then the sum is assigned 0. This is because if (-8) + (-7) is a case then the sum is -15 which should not be included.

Algorithm

The algorithm for Kadane’s Algorithm is as follows:

  1. Initialize prevSum to 0, initialize currentSum to the minimum value of a 32-bit Integer
  2. Add array element in the prevSum
  3. Check if prevSum>currentSum:
  • If true, then the sum is greater thus, assign prevSum to currentSum(the answer variable )
  • If false, then no change in currentSum

4. If the prevSum was less than 0 then prevSum=0 because if the negative number is included then the sum is negative. In the next iteration, if a positive number is added to the sum (which is negative ), the overall sum is reduced.

Example: if prevSum=-4 and current element is 5 then sum = -4 + 5 = 1 which is less than the sum by including only the current element which is 5.

Code Implementation

Below is the Java code for Kadane’s Algorithm to find the maximum sum Subarray:

class Solution {
    public int maxSubArray(int[] nums) {
        int currentSum=Integer.MIN_VALUE;
        int prevSum=0;
        for(int i=0;i<nums.length;i++){
            prevSum+=nums[i];
            if(prevSum>currentSum){
                currentSum=prevSum;
            }
            if(prevSum<0)prevSum=0;
        }
        return currentSum;
    }
}

write your code here: Coding Playground

Suppose the given array is: [-2,1,-3,4,-1,2,1,-5,4]. Here the maximum sum subarray is [,4,-1,2,1] with the sum as 6.  Therefore, we declare two variables prevSum and currentSum. currentSum will store the actual answer and prevSum stores the sum of the elements in each iteration. The following observations are made:

Iterations

  • Iteration 1

prevSum= -2

prevSum>currentSum, thus currentSum=-2

prevSum<0 thus, prevSum=0

  • Iteration 2

prevSum= 1

prevSum>currentSum(-2) thus, currentSum=1

prevSum<0 is false thus prevSum=1

  • Iteration 3

prevSum= 1+ (-3)= -2

prevSum>currentSum is false thus currentSum=1

prevSum<0 thus prevSum=0

  • Iteration  4

prevSum=4

prevSum>currentSum thus currentSum=4

prevSum<0 is false thus prevSum=4

  • Iteration 5

prevSum= 4+ (-1)=3

prevSum>currentSum is false thus currentSum=4

prevSum<0 is false thus prevSum=3

  • Iteration 6

prevSum= 3+2 = 5

prevSum>currentSum thus currentSum=5

prevSum<0 is false thus prevSum=5

  • Iteration 7

prevSum= 5+1 = 6

prevSum>currentSum thus currentSum=6

prevSum<0 is false thus prevSum = 6

  • Iteration 8

prevSum= 6+ (-5)= 1

prevSum>currentSum is false thus currentSum=6

prevSum<0 is false thus prevSum = 1

  • Iteration 9

prevSum= 1+4= 5

prevSum>currentSum is false thus currentSum=6

prevSum<0 is false thus prevSum =  4

Therefore, the answer was stored in the currentSum which is returned in the end. Thus, the maximum sum of a subarray can be found using Kadane’s Algorithm.

Sample Output for the above code is: