Introduction
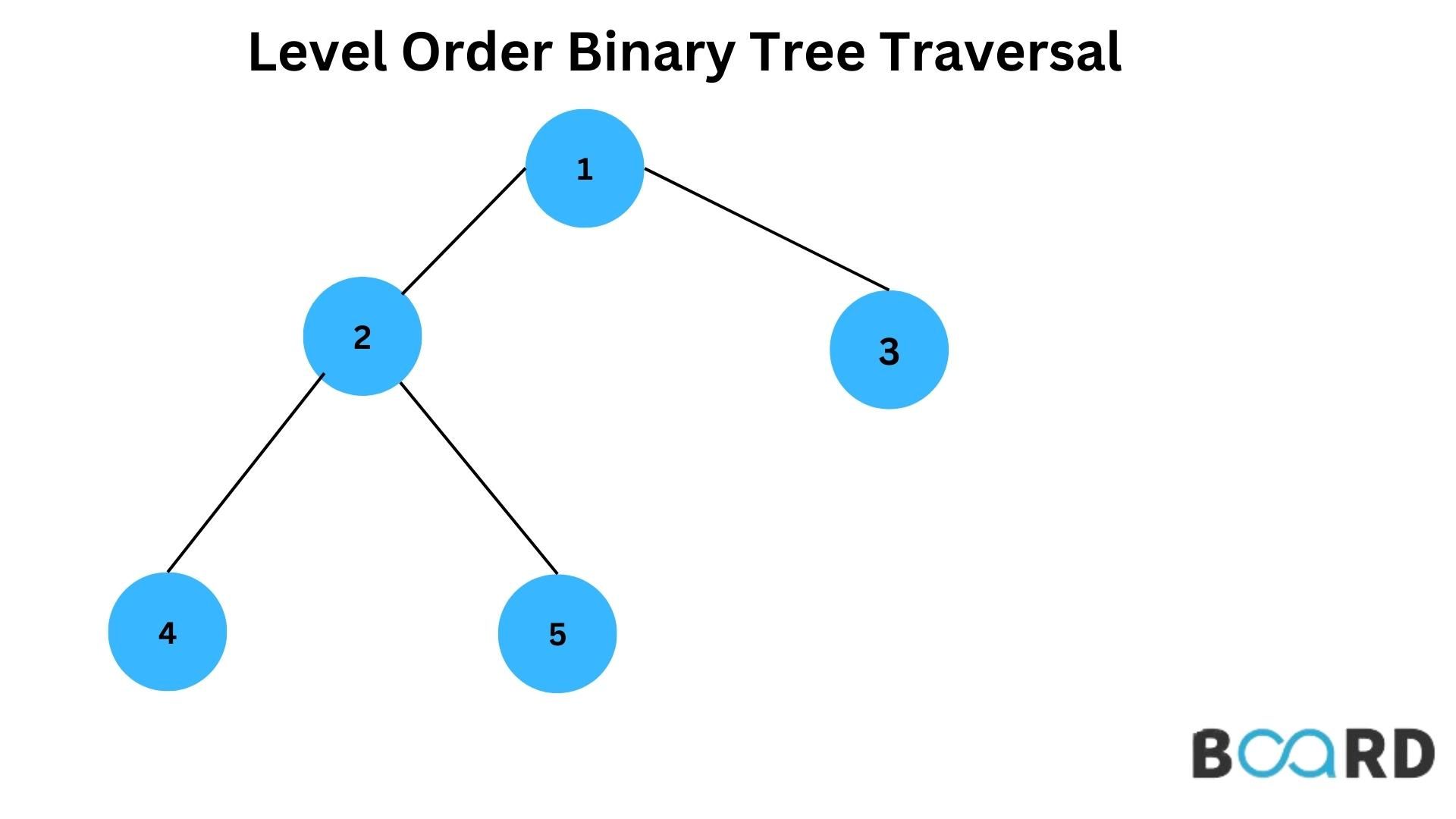
In this article, we will be learning the level order traversal. This is one of the most important topics to traverse graphs. You will be given a root of the tree and then you have to print its level order traversal.
There are two methods to traverse a tree using level order. We will be learning both methods in this article:
Method 1: Using Recursion
#include <iostream>
using namespace std;
class node {
public:
int data;
node *left, *right;
};
node* newNode(int data);
node* newNode(int data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
int height(node* node) {
if (node == NULL)
return 0;
else {
int lheight = height(node->left);
int rheight = height(node->right);
if (lheight > rheight) {
return(lheight + 1);
}
else {
return(rheight + 1);
}
}
}
void CurrentLevel(node* root, int level) {
if (root == NULL)
return;
if (level == 1)
cout << root->data << " ";
else if (level > 1) {
CurrentLevel(root->left, level-1);
CurrentLevel(root->right, level-1);
}
}
void LevelOrder(node* root) {
int h = height(root);
int i;
for (i = 1; i <= h; i++)
CurrentLevel(root, i);
}
int main() {
node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
LevelOrder(root);
return 0;
} |
Time Complexity: O(N2), where N is the number of nodes in the skewed tree. So the time complexity of printLevelOrder() is O(n) + O(n-1) + O(n-2) + .. + O(1) which is O(N2).
Auxiliary Space: O(N) in the worst case. For a skewed tree, printGivenLevel() uses O(n) space for the call stack. For a Balanced tree, the call stack uses O(log n) space, (i.e., the height of the balanced tree).
Method 2: Using Queue
- Create an empty queue q and push root in q.
- Run While loop until q is not empty.
- Initialize temp_node = q.front() and print temp_node->data.
- Push temp_node’s children i.e. temp_node -> left then temp_node -> right to q
- Pop front node from q.
#include <bits/stdc++.h>
using namespace std;
// A Binary Tree Node
struct Node {
int data;
struct Node *left, *right;
};
// Iterative method to find height of Binary Tree
void printLevelOrder(Node* root)
{
// Base Case
if (root == NULL)
return;
// Create an empty queue for level order traversal
queue<Node*> q;
// Enqueue Root and initialize height
q.push(root);
while (q.empty() == false) {
// Print front of queue and remove it from queue
Node* node = q.front();
cout << node->data << " ";
q.pop();
/* Enqueue left child */
if (node->left != NULL)
q.push(node->left);
/*Enqueue right child */
if (node->right != NULL)
q.push(node->right);
}
}
// Utility function to create a new tree node
Node* newNode(int data)
{
Node* temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
// Driver program to test above functions
int main()
{
// Let us create binary tree shown in above diagram
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Level Order traversal of binary tree is \n";
printLevelOrder(root);
return 0;
} |
Time Complexity: O(N) where n is the number of nodes in the binary tree.
Auxiliary Space: O(N) where n is the number of nodes in the binary tree.
Hope this article gave you a clear understanding of the concept. To check out similar topics, do visit the Discussion Forum and Board Infinity Blogs.