- Explore [has_child]
- All Courses [subitem]
- AI Career Platform [subitem]
- Hire form us [subitem]
- 1:1 Coaching/Mentoring [subitem]
- Job Board [subitem]
- Institute Partnerships [subitem]
- Resources [has_child]
- Master Classes [subitem]
- Discussion Forum [subitem]
- Coding Playground [subitem]
- Free Courses [subitem]
- Topics [has_child]
- Data Science [subitem]
- Software Development [subitem]
- Python [subitem]
- Programming [subitem]
- Digital Marketing [subitem]
- Web Development [subitem]
- Career Development [subitem]
- Success Stories
Advanced Algorithms and Problem Solving Techniques
How To Start Competitive Programming - A Complete Guide
A Quick Guide to Breadth-First Search
Depth First Search (DFS) with Explanation and Code
Difference Between BFS and DFS (with code and diagrams)
How to Perform Level Order Traversal?
A Quick Guide to Backtracking Algorithm
Solving N Queens Problem using Backtracking
Quick Guide to Divide and Conquer Algorithm
Longest Increasing Subsequence Problem
Quick Note - Greedy Programming v/s Dynamic Programming
Coin Change Problem: DP and Recursion Approach
A Definitive Guide to Knapsack Problem
How to Solve Subset Sum Problem?
Understanding Huffman Coding in detail
Understand the working of KMP Algorithm
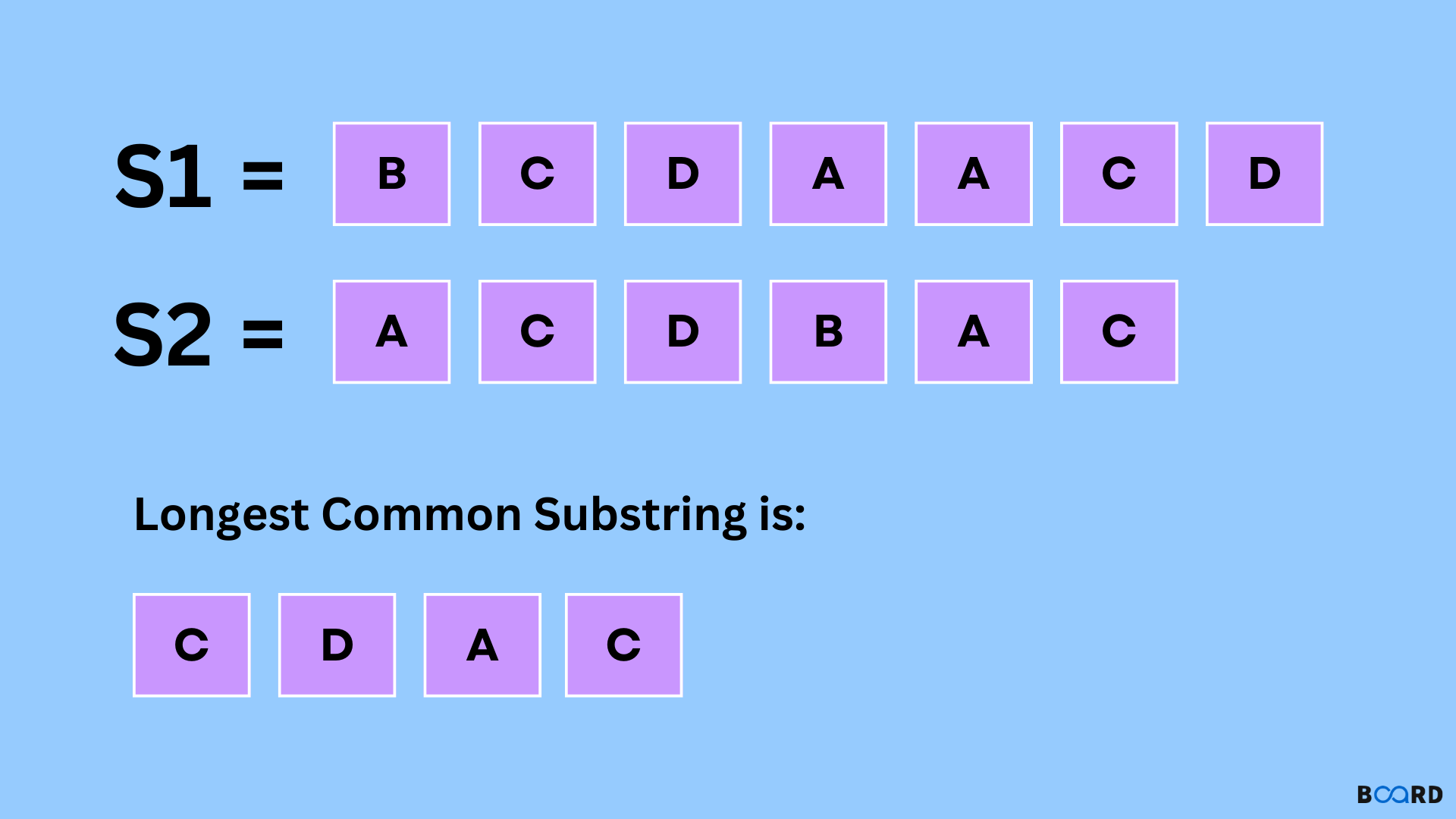
Longest Common Substring Problem
Longest Common Subsequence problem: solved
A Quick Guide to Manacher's Algorithm
Learning About Bipartite Graphs
Graph Coloring Problem: Explained
Detect Cycle in Direct Graph
Directed Acyclic Graph: Representation
Prim's Algorithm: Explanation, Code, and Applications
Working of Kruskal's Algorithm
Prims and Kruskal algorithm for Maximum Spanning Tree
Bellman Ford Algorithm in detail with code
Floyd-Warshall Algorithm and its Implementation
Understand Travelling Salesman Problem
Branch And Bound Algorithm: Explained
How to Evaluate Postfix Expression
Introduction to Round-Robin Scheduling
Disjoint set (Union find Algorithm)
State Space Reduction in Algorithms
Apriori Algorithm
What is A* Search Algorithm?
Problem Statement
Assume that S1 and S2 are two strings and that:
- S1 = akfdcmejf
- S2=”sfkpdcnmej”
The "kdcmej" character is the Longest Common Subsequence (LCS) between these two strings. It's not a given that a subsequence will be contiguous just because it's a subsequence.
Subsequence
Take the sequence S = [s1, s2, s3, s4,..., sn] into consideration.
If and only if it can be derived from the S deletion of some components, a sequence Z = z1, z2, z3, z4,...,zm> over S is a subsequence of S.
Common Subsequence
Let's say that X and Y are sequences spanning a limited number of elements. If Z is a subsequence of both X and Y, then Z is a common subsequence of X andY.
Theory
The longest common subsequence challenge aims to identify a common subsequence of all the given sequences that has the maximum length.
A well-known topic in computer science, the most extended common subsequence problem serves as the foundation for data comparison tools like the diff-utility and has uses in bioinformatics.
Algorithm
Algorithm: LCS-Length-Table-Formulation (X, Y) |
Algorithm: Print-LCS (B, X, i, j) |
Top-Down Approach: Using C++
// Board Infinity |
Bottom-up Approach: Using C++
// Board Infinity |
