Introduction
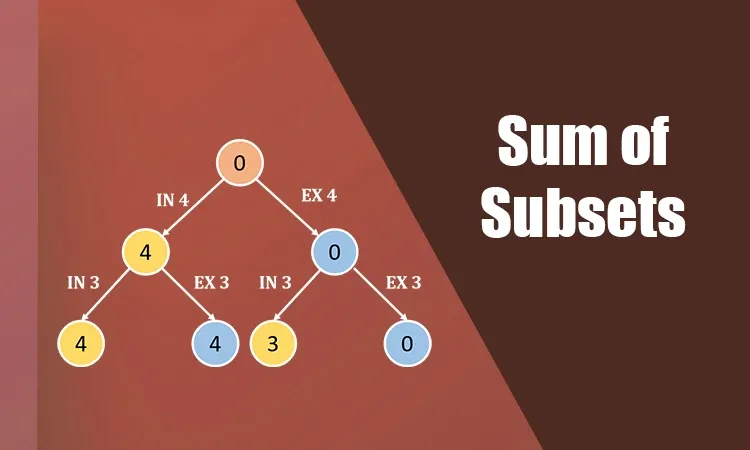
Finding a subset' of the provided array A = (A1 A2 A3...An), in which the items of the array A are n positive integers, in such a way that a'A and the sum of the elements of such a subsets is equal to a certain positive integer S, is the goal of the subset-sum problem. This is a NP-hard problem. Given that there are several strategies for addressing it, subset-sum is an optimizing issue. With a manageable time complexity, subsets can be handled using dynamic programming and backtracking.
Problem Statement: Determine if there is a non-empty subset of the positive set of integers that sums to the number k.
Input:
A = { 3, 7, 8, 5, 2 }
k = 14
Output: Subset with sum=14 exists -> Subset { 7, 2, 5 } sums to 14
Efficient Dynamic Approach
- A dynamic approach to problem resolution would be ideal for such issues.
- By starting with smaller subproblems and working our way up, we can solve larger subproblems.
- If a subset with sum j can be discovered using items up to the first I items, the bottom-up method that follows computes T[i][j] for each 1 = I = n and 1 = j = sum is true.
- It makes use of the previously computed lower values of I and j to prevent repeated calculations, hence reducing the time complexity.
Implementation Code
Complexity Analysis
Time Complexity: O(N * sum)
Here, N = size of the array.
Space Complexity: O(N * sum)
Here, N = size of the array.