Understanding Huffman Coding in detail

Introduction

You will discover how Huffman Coding functions in this article. Working examples of Huffman Coding in C++ are also provided. Data can be compressed using the Huffman coding method without losing any of the information. David Huffman was the one who first created it. In general, Huffman Coding is helpful for compressing data that contains frequently occurring characters.

How It Works

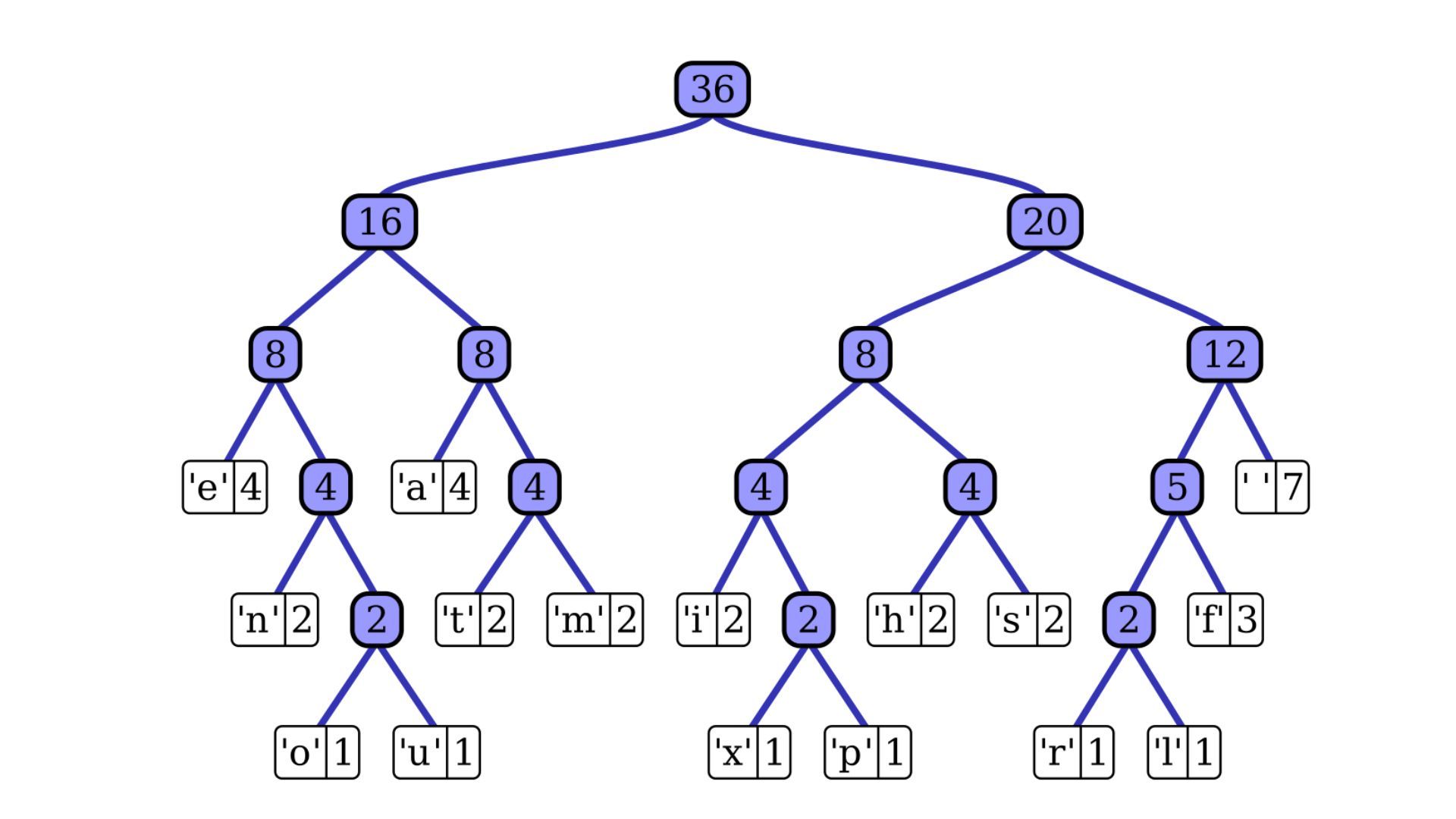
A character takes up 8 bits. Assuming a string contains 15 characters, a total of 8 * 15 = 120 bits are needed. By using the Huffman Coding method, we can reduce the string's size. Using the character's frequency information, Huffman coding first constructs a tree before generating code for each character. Data must be decoded after it has been encoded. Using the same tree, decoding is performed.

Using the idea of prefix code, or the rule that a code associated with a character should not appear in the prefix of any other code, Huffman coding prevents any uncertainty in the decoding process. The tree that was planted above contributes to keeping the property up.

Steps:

Two different types of encoding exist:

1. Fixed-Length Encoding: With this method, a fixed-length binary code is used to represent each character.
2. The method known as variable-length encoding uses a binary code of varying length to represent each character.
   

From this example it is clear that the string had a total length of 120 bits before encoding. The size is decreased to 32 + 15 +28 = 75 after encoding.

The following steps are used to complete Huffman coding:-

1. Make a priority queue Q with each special character in it.
2. then order them according to increasing frequency.
3. For each of the distinct characters:
4. Extract the minimum value from Q, then create a new node and assign it to the left
5. Extract the minimum value from Q as a child of newNode, then assign it to the right
6. Child of newNode adds up these two minimum values and applies the result to the value of newNode.
7. Add this newNode to the tree and then return to the rootNode

Decoding

A portion of an encoded message like "00101001" can be decoded in a variety of ways. This can be taken in at least two different ways:

• Code '0 0 10 10 01' -> aaddc
• Code '0 010 10 01' ->abdc

The issue with variable-length encoding is that we cannot decode the message or text in a singular way. We must make sure that the codes assigned to every character are prefix codes in order to ensure efficient decoding.

Code

Complexity Analysis

Based on their frequency, each unique character requires (nlog n) to encode. The complexity of obtaining the minimum frequency from the priority queue is O, and it occurs 2*(n-1) times (log n). Hence, complexity is generally addressed as O (nlog n) for Huffman Coding.